Scoring in a complete search system

Introduction

Previously, I described TD-IDF weighting in Content-based recommender system; actually, this is also very useful in a real information retrieval system. There is a scoring algorithm called Cosine Score for query system.(In natrual, it is same technique with TD-IDF weighting)

CosineScore (q)
float Score[N] = 0
Initialize Length[N]
for each query term t in q
do calculate w_{t,q} and fetch postings list for t
	for each pair(d,tf_{t,d}) in postings list
	do Scores[d] += wf_{t,d} * w_{t,q}

Read the array Length[d]
for each d
do Scores[d] = Scores[d] / Length[d]
return Top K components of Scores

In a typical setting we have a collection of documents each represented by a vector, a free text query represented by a vector, and a positive integer K. We seek the K documents of the collection with the highest vector space scores on the given query.

The array Length holds the lengths (normalization factors) for each of the N documents, whereas the array Scores holds the scores for each of the documents. The outest loop repeats the updating of Scores, iterating over each query term t in turn.

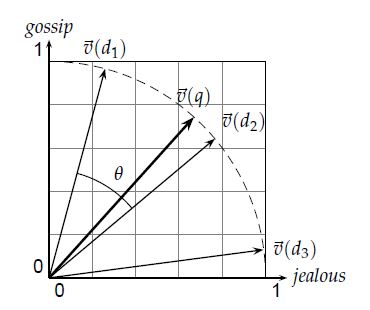
Actually, in this approach, we are treating query as a vector. Here is a example : gossip jealous.

Note: this approach loses the relative ordering of the terms in each document. It is a bag of words representation.

####Efficient Scoring For the purpose of ranking the documents matching this query, we are really interested in the relative(rather than absolute) scores of the documents in the collecitonl. So, it suffices to compute the cosine similarity from each document unit vector $v(d)$ to $V(q)$(in which all non-zero components of the query vector are set to 1), rather than to the unit vector $v(q)$. For any 2 documents $d_1,d_2$

$V(q)\cdot v(d_1) > V(q) \cdot v(d_2) \Leftrightarrow v(q) \cdot v(d_1) > v(q) v(d_2)$

FastCosineScore(q)
float Scores[N] = 0
for each d
do Initialize Length[d] to the length of doc d
for each query term t in q
do calculate w_{t,q} and fetch postings list for t
	for each pair(d, tf_{t,d}) in postings list
	do add wf_{t,d} to Scores[d]

Read the array Length[d]
for each d
do Divide Scores[d] by Length[d]
return Top K components of Scores[]