Consistent Hashing
I. Problems in naive approach
Naive method: Suppose we have a cluster of $n$ computers. We number the computers $0,1,2,\ldots,n-1$, and then store the key-value pair $(k,v)$ on computer number $hash(k)$ $mod$ $n$. If we’re using a good hash function, then $hash(k)$ $mod$ $n$ is a uniform across $0,1,2,\ldots,n-1$ for any reasonable distribution of keys. This ensures our distributed dictionary is spread evenly across the computers in our cluster, and doesn’t build up too much on any individual computer.
Naive hash-based distributed dictionaries are simple, but they have serious limitations. Imagine you are using a cluster of computers to crawl the web. You store the results of your crawl in a distributed dictionary. But as the size of the crawl grows, you will want to add machines to your cluster. Suppose you add even just a single machine. Instead of computing $hash(k)$ $mod$ $n$, we are now computing $hash(k)$ $mod$ $n$. This result is that each key0value pair will get reallocated completely at random across the cluster. You’ll end up moving a fraction $n/(n+1)$ of your data to new machines.
II. Consistent Hashing
Suppose we have $n$ machines and we number them as $0, \ldots, n-1$. If the hash function has range $[0,R)$ then we scale the hash funciton via $hash(x)/R$, so that hash function maps into the range $[0,1)$
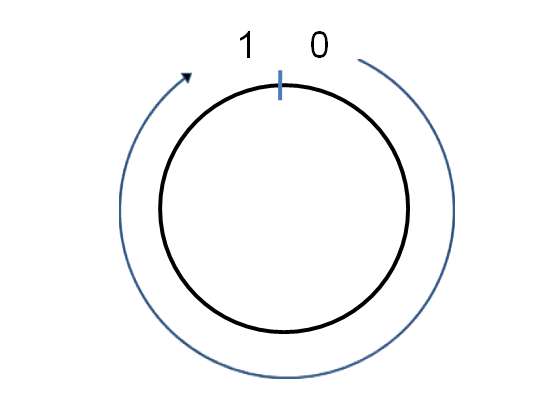
Then we can hash machine numer $i$ to a point $hash(i)$ on the circle, for each machine in the range $i=0 \ldots n-1$. Here’s on example for $n=3$ machine cluster:
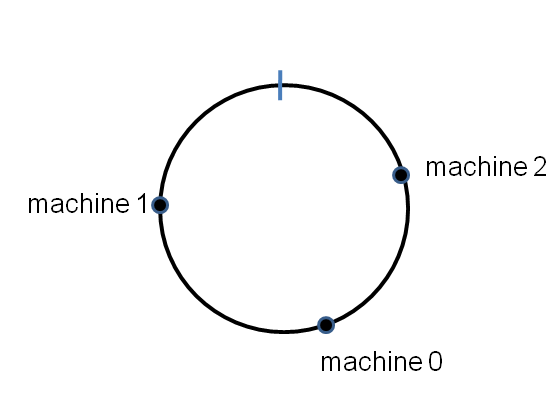
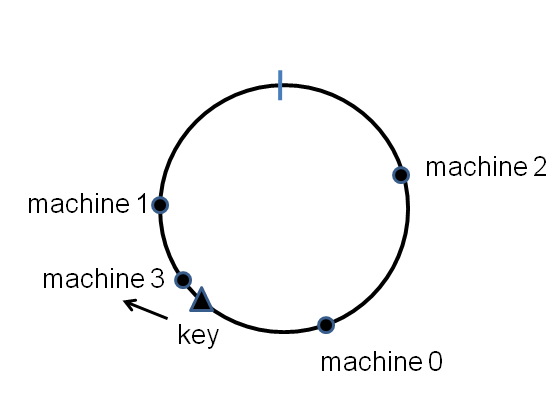
The points will be randomly distributed around the circle. Now we want to store a key-value pair in this distributed dictionary. We simply hash the key onto the circle, and then store the key-value pair on the first machine that appears clockwise of the key’s hash point. E.g for the key shown here, the key-value pair is stored on machine number 1:
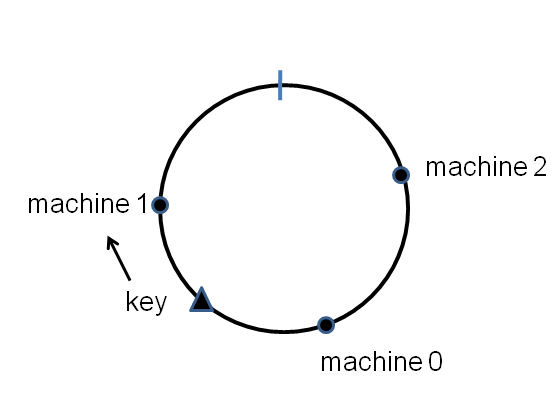
As long as we have a good hash function, a fraction roughtly $\frac{1}{n}$ of the key-value pairs will get stored on any single machine.
Now, what if we add an extra machine into the cluster? It goes to the point $hash(n)$. Most of the key-value pairs are completely unaffected by this change. But we can see that some of the key-value pairs that were formerly stored on machine 1 will need to be moved to the new machine. But the fraction that needs to be moved will typically be $\frac{1}{n+1}$ of the total, a much smaller fraction thatn was the case for naive hashing.