Data Infrastructure - Graph Traversal Pattern I
I found a very good paper which describe the graph traversal pattern and its underlying infrastructure to go.
Introduction
Today, every tech company talks about big data. But what exactly those companies’ data look like? Take Facebook as an example. Facebook owns a social network data which take people as nodes and friendships as edges. Facebook is a People Graph. For Google, it takes web documents as nodes and hyperlinks as edges. The big data Google has is a Knowledge Graph. For Pinterest, it takes 2 nodes: people and pin boards, takes interests as edges.
With all these examples, we can find theoretically they are all “Property Graphs” with attributed edges. This series of posts will discuss topics about the data infrastructure and the common operation(purpose) on top of the infrastructure. Basically, the most common operation is “Recommendation”.
Constraint of Relational Database
Relational databases maintain a collection of tables. Each table can be defined by a set of rows and a set of columns. Traditionally, rows denote objects and columns denote properties/attributes. Usually, a problem domain is modelled over multiple tables in order to avoid data duplication. This process is known as data normalization . In order to unify data in separate tables, a “join” is used. A join combines two tables when columns of one table refer to columns of another table. Maintaining these references in a consistent state is know as a referential integrity.
An example described in that paper: we have 2 tables. One is people table and another is friendship table. We want to get all friends of Alberto Pepe.Usually, relational database has tree-structured index built on top of table.(Like B+ tree), which can enable log n query complexity.
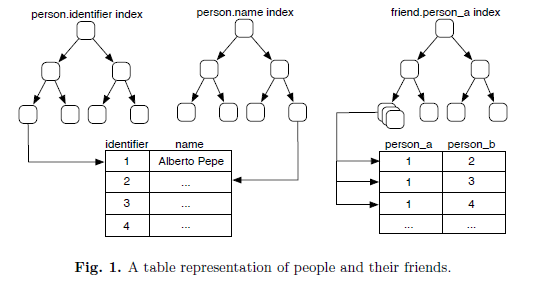

The final operation yields the names of Alberto’s friends. This example elucidates the classic join operation utilized in relational databases. By being able to join the person and friend table, its possible to move from a name efffect , to the person, to his or her friends, and then finally to their names. In effect, the join operation forms a graph that is dynamically constructed as one table is linked to another table. The limitation is that this graph is not explicit in the relational structure , but instead must be inferred through a series of index-intensive operations. Moreover, while only a particular subset of the data in the database may be desired, all data in all queried tables must be examined in order to extract the desired subset.
The read-time is fast for a search, as the index grow larger with the growth of the data and as more join operations are used, this model becomes inefficient. At the limit, the inferred graph that is constructed through joins is best solved, graph database .
The Graph as an Index
Most of graph theory is concerned with the development of theorems for single relational graphs. A single-relational graph maintains a set of edges, where all the edges are homogeneous. For example, all edges denote friendship or kinship, but not both together within the same structure. In application, complex domain models are more conveniently represented by multi-relational, property graphs. The edges in a property graph are typed or labeled and thus, edges are heterogenous. For example, a property graph can model friendship, kinship, business, communication,etc. relationships all within the same structure. Moreover, vertices and edges in a property graph maintain a set of key/value pairs. These are known as properties and allow for the representation of non-graph data,like the name of a vertex, the weight of an edge. Formally, a property graph can be defined as , where edges are directed, edges are labeled( : ), and properties are a map from elements and keys to values.
Now let’s see the graph database apporach in previous example.
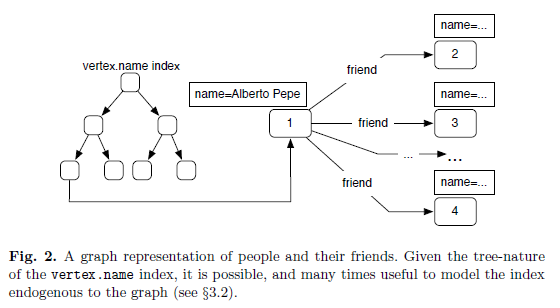

In a graph, database, there is no explicit join operation because vertices maintain direct references to their adjacent edges. In many ways, the edges of the graph serve as explicit, “hard-wired” join structures. The act of traversing over an edge is the act of joining. What makes this more efficient in a graph database is that traversing from one vertex to another is a constant time operation.